Deterministik kaos kuramları

Bilim, özellikle fizik, kimya, biyoloji ve kozmoloji, evrenin düzenli hareketlerini belirleyen basit doğa kanunlarını matematiksel modeller ile ifade eder. Newton kanunları kütle-çekim alanları içinde bulunan iki cismin birbirlerini kütlelerinin çarpımı ile doğru, aralarındaki uzaklığın karesi ile ters orantılı çektiğini söyler. Bu kanununa göre herhangi bir hareketin başlangıç şartları, yani başlangıç konumu ve ilk hızı biliniyorsa, cismin ne zaman nerede ve hangi hızda olacağı hesaplanabilir. Kuzey Amerika kıtasından atılan bir füze ile Pasifik Okyanusu'ndan atılan bir füzeyi Hint Okyanusu üzerinde 15000 metre yükseklikte 30 dakika sonra çarpıştıran teknoloji, Newton kanunlarına dayandırılarak geliştirilmiştir. Yerküre çevresinde çok sayıda yapay uydu çeşitli amaçlar ile dönüp durmaktadır. Uyduların ve füzelerin nerede ne zaman bulunacakları hesap edilebilmekte, daha da ilerisi komşu gezegenlerine uydular gönderilerek bilgi toplanabilmektedir. Bütün gelişmeler klasik fiziğin belirlemeci (determinist) özelliğinden kaynaklanmaktadır. Newton ve Maxwell kanunlarının birinci dereceden diferansiyel denklemler ve çözümlerinin analitik oluşu klasik fiziğe determinist bir özellik sağlamıştır.

Deterministik kaos modellerinin doğuşu

Doğa lineer bir sistem değildir. Fiziksel, kimyasal ve biyolojik olaylar ancak birinci yaklaşıklıkla lineer denklemler ile ifade edilebilir. Makroskopik boyutlarda determinist olan doğa, atomik boyutlara inildiğinde probabilistik (olasılıkçı) olur. Mikroskopik boyutlarda bir parçacığın en basit fiziksel özelliği olan konumu bile ancak bir olasılık dahilinde belirlenebilir. Heisenberg belirsizlik ilkesi, bir elektronun veya en genel anlamda atomik boyutlarda, bir sistemin hızının ve konumunun aynı anda ölçülemeyeceğini söyler. Makroskopik boyutlarda zamanın tek yönlü akışını belirleyen entropi, mikroskopik boyutlarda olasılık dalgasının çökmesi gibi zamanın yönünü kesin olarak belirleyemez. Kaos, fiziğin determinist kanunları ile değişimin kanunları arasında bir köprü kurmaya çalışır. Küçüklerin dünyası kuantum fiziği ile büyüklerin dünyası klasik fiziğin sınırlarında meydana gelen olayların matematiksel modellerinin kurgulanmasında karşılaşılan güçlükler, deterministik kaos modellerini doğurmuştur.

Doğa, lineer olmayışını kaotik davranışlar ile gösterir. Kaos, dinamik olaylar ile tanımlıdır. Bir sistemin zaman içinde değişimi klasik fizik kanunlarına göre gerçekleşmiyorsa veya bu kanunlar değişimi hesap edemiyorsa olay kaotiktir. Bir sistem kendini karakterize eden fiziksel büyüklükler ile belirlidir. Herhangi bir anda sistemi belirleyen büyüklükler biliniyorsa sisteme ait tüm dinamikler, klasik fiziğe göre hesap edilebilir. Rüzgârda dalgalanan bir bayrağı göz önüne alınız. Dikdörtgen şeklindeki bayrağın herhangi bir noktasının saniyenin onda biri kadar kısa bir süre sonra nerede olacağını hesap edebilir misiniz? Bu soru size yarar bağlamında saçma gelebilir. Benzer şekilde rüzgârda salınan ağaç yapraklarının belli bir süre sonra nerede olduğunu hesap edebilmek için çok yüksek bellekli bilgisayarlar bile yeterli olamazlar. Şimşek çaktığında çok ani olarak bir ışıldama görürüz. Şimşeğin bir saniyenin binde biri kadar kısa bir süre sonra nerede olacağını hesap edebilir miyiz? Hayır edemeyiz. Diğer yandan Ata Kule’nin tepesinden serbest bırakılan bir taşın ne zaman, nerede ve hangi hızda olacağını hesap edebiliriz. Bir köprüden hızla akan ırmağın üzerinde nereye gideceği kestirilemeyen yaprakları gözleyiniz. Biri veya birkaçı küçük bir girdap tarafından yakalanır, bir iki dönüş yapar, bazıları kurtulur, sonra başka bir girdaba kapılmadan belli bir süre gider, sonra yine kapılır ve sonunda gözden kaybolur. Füzeleri çarpıştıran matematik, küçücük bir yaprağın hareketini aynı hassasiyetle hesap edemez. Kaos işte bu hesaba gelmeyen olaylar demektir. Bu olayları anlatmak için çok yararlı bir benzetme yaygın olarak kullanılır. Brezilya’da bir kelebek kanat çırpsa Pasifik Okyanusu'nda bir kasırga kopabilir.

Kaos sürekli bir dengesizlik durumudur. Bir sisteme birden fazla kuvvet etkiyorsa ve kuvvetlerin tek bir bileşeni alınamıyorsa, sistem genel anlamda kaotiktir. Bütün bu güçlüklere rağmen kaotik olayların deterministik yanları bulunabilir. Sistem ne kadar kaotik bir durumda bulunursa bulunsun, önemli olan probabilité ve klasik istatistik kanunlarını kullanarak deterministik bir kaos teorisi kurgulamaktır. Deterministik kaos kuramının amacı düzensizlikler içinde gizli olan, görünmeyen düzenli yapıları ortaya çıkartmaktır. Acaba nehirde kendi başına yüzüp giden yaprağın veya okyanuslar üzerinde oluşup kıyılara korku saçan kasırgaların hareketlerinde düzenli olan büyüklükler var mıdır? Deterministik kaos kuramı bunların peşindedir.

Gaz moleküllerinden oluşan bir sistemi basınç, hacim ve sıcaklık belirler. En genel anlamda sistemler basınç, hacim, sıcaklık gibi fiziksel büyüklükler ile karakterize edilir. Eğer sistemi tanımlayan büyüklüklerin herhangi bir andaki değerleri biliniyorsa sistemin değişimi ile ilgili tüm bilgiler hesap edilebilir. Deterministik kaotik teorilerde sistemin herhangi bir parametresindeki değişim, sistemi belirleyen büyüklüklere ait bilgi ile art arda geri beslenerek matematiksel bir modele dönüştürülür. Örneğin balıkçılardan ve kirlenmeden soyutlanmış bir gölde birbirlerine besin zinciri ile bağlı iki balık türünü göz önüne alalım. Balıklar sadece çevre ve kendi fizyolojik koşulları altında hızla çoğalır. Bu koşullar altında göldeki balık sayısı artar. Eğer balık sayısı belli bir eşik değeri geçerse aralarında besin bulma bağlamında ciddi bir problem baş gösterir. Bu duruma ulaşıldığında balık sayısında artma gözlenemez. Benzer durumlar bitkiler için de söz konusu olabilir.

Düzensizlik problemi

Düzensizlik problemini basit bir matematik kurguya yansıtmak mümkündür. Lisede gösterilen matematiğin sınırları içinde kalarak bu kurguyu aşağıda anlatmaya çalıştık. Fonksiyonlardan korkmayarak biraz dikkat gösterecek olursanız olayın gidişatını anlamakta zorluk çekmezsiniz.

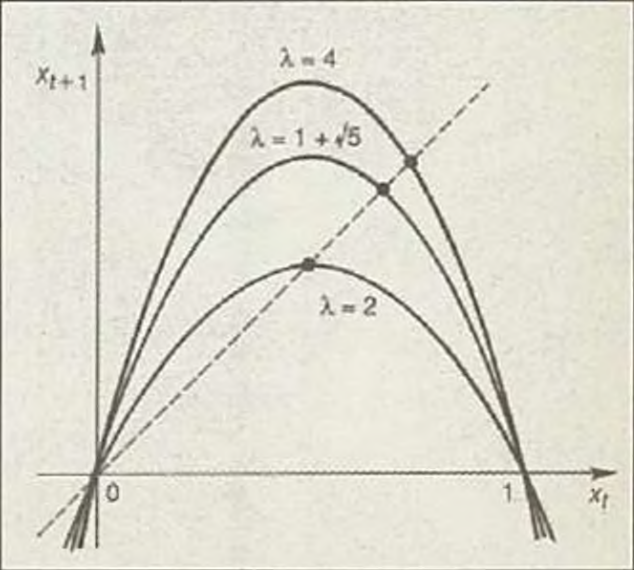
Sistemi karakterize eden değişkeni x_t ile gösterelim. Burada alt indis t bir tam sayı olup x değişkeninin art arda yapılan ölçümlerine tekabül eder. Anlaşılacağı gibi t fiziksel zaman ölçümünü göstermez, t ve t+1 art arda gelen iki ölçümü gösterir. Eğer bir popülasyon problemi varsa t art arda gelen nüfus indeksi demektir. t=0 sistemin içinde bulunduğu durumu, x₀ bu duruma tekabül eden ölçümü ifade eder. Eğer bir nüfus problemi söz konusu ise x₀ başlangıç nüfusunu temsil eder. Geleceği belirleme, ölçülen değişkenin x_t değerini hesap edebilmektir. İndeks yani t büyüdükçe x değişkeninin sonsuzdaki değeri belirlenmiş olur. Dolayısıyla deterministik bir model elde edilir. Ancak bu belirlemeyi yapabilmek için x değişkeninin t ve t+1 indeksi ile belirli durumları arasındaki ilişki bir bağıntı ile ifade edilir. Bu ilişkiyi x_t+1= f(x_t)  (1) şeklinde bir fonksiyon yansıtır. Burada f fonksiyonu, t ve t+1 indeksleri ile belirli art arda gelen ölçümleri birbirine bağlar. Görüldüğü gibi x_t+1 değeri x_t değerine bağlıdır. Buna göre Eş(1) ile verilen fonksiyon deterministiktir ve sisteme ait bilgileri içerir. Art arda gelen ölçüm değerlerini birbirine bağlayan f(x) fonksiyonunun açık şekli, olayların gözlenmesi ile tespit edilebilir. Sistemi karakterize eden art arda ölçümler arasındaki ilişki parametrik bir bağıntı ile verilir. x_t= f(λx_t) = λx_t (1-x_t)  (2). Burada λ geri-besleme parametresidir. Sistemin zaman içinde ilerleyişinde geri besleme bilgisinin etkisini yansıtır. Geometrik olarak λ’nın değişmesi f fonksiyonunun değişmesi ile eş anlamlıdır. Eş(2) ile verilen fonksiyonun grafiği x_t değişkenine göre bir paraboldür. λ’nın değişik değerleri için grafik şekilde gösterilmiştir.

Grafik x_t+1 karşı x_t olarak çizilmiştir. x_t+1= x_t diagonalinin üstünde kalan eğriler için x_t+1 öçümleri x_t ölçümlerinden daha büyük, diagonalin altında kalan eğrilerde ise daha küçüktür. Fonksiyonun grafiği diagonalin altında küçük x_t üstünde büyük x_t’leri ifade eder. Ölçüm değerlerini gösteren x_t paremetresinin 0 ve 1 arasında değişmesi problemin genelliğine bir sınırlama getirmez. Bu arada herhangi bir ölçüm, başlangıç değeri olarak kabul edilebilir. Önemli olan bu kabulden sonra art arda gelen değerlerin nasıl değiştiğini belirleyebilmektir. Şimdi akla gelen soru x₀’ın ve λ’nın fonksiyonu olarak x_t’nin hesap edilip edilemeyeceğidir. Eş(1)’den x₁=λx₀(1-x₀) bulunur. Aynı bağıntıyı kullanarak x₂=λ(λ(x₀(1-x₀)(1-λx₀))) ve x₃=λx₂(1-x₂)= λ(λ(λx₀(1-x₀)(1-λx₀(1-x₀)))(1-λ(λx₀(1-x₀)(1-λx₀(1-x₀)))))  (3).

Görüldüğü gibi üçüncü mertebeden geri beslenen bir sistemi belirlemek dahi hesap edebilme sınırlarına dayanır. Ancak bilgisayar iterasyon yöntemleri ile bir sistemi karakterize eden herhangi bir fiziksel büyüklüğün zaman içinde gelişimini nümerik olarak hesaplamak olasıdır. Geri besleme bilgisini kullanarak kaotik bir sistemin gelişimini belirlemek deterministik kaos yöntemlerinden sadece biridir. Şekil 2’de λ keyfi iki değer arasında salınırken Eş(2) denkleminin verdiği bilgisayar benzeşimi gösterilmiştir. Renkler hareketin nasıl düzenli geliştiği hakkında bir bilgi vermektedir (koyu mavi şeritler). Açık mavi ve beyaz bölgeler karmaşık harekete karşı gelmektedir.

Burada önemli olan t’nin artan değerleri için x_t’yi hesaplamaktır. Sistemin başlangıç durumunu karakterize eden x₀’dan başlayarak geçerli bir λ için, x₁=f(λ,x₀), x₂=f(λ,x₁), x₃=f(λ,x₂) birbirlerini geri besleyen değerler ile x_t bulmaktır. Her ara işlemde x’in tüm geçmiş değerleri değil sadece bir önceki aşamaya ait değeri girdi olarak kullanılır. Bunun sonucu olarak sistemi karakterize eden fiziksel büyüklük x’in x₀,x₁,x₂,x₃,..…,x_1000000,...…,x_t değerleri bilgisayar iterasyon yöntemleri ile hesap edilebilir. Dolayısıyla sistemin her aşamasına ait bilgiyi ondan sonra gelecek aşamaya girdi olarak vererek, kaotik olaylardaki düzeni belirleyen bir matematik teknik geliştirilir. Birçok klasik dinamik sistemlerde kaotik durumlar ortaya çıkar. Bilgisayarlarda geliştirilen çeşitli hesap teknikleri ile sistemlerde kaosu meydana getiren değişim davranışları, belli bir hata ile hesap edilebilmektedir. Bilgisayarlar geniş bellek ve logik işlemcileri ile günümüzde, lineer olmayan sosyal veya doğa olaylarına analiz imkânı sağlamıştır. Kaotik olayları bilgisayarlar ile analiz etmek, bir yerde matematik deneyleri yapmaya benzer.

Deterministik kaos kuramlarının matematiksel yapısı

Deterministik kaos kuramının dayandığı matematiksel yapı basit olarak, bilardo toplarının hareketi ile açıklanır. Bilardo masası bir düzlem olduğuna göre birine dik iki eksen, örneğin x ve y eksenleri ile belirlenir. Top basit bir sistem olarak kabul edildiğinde sistemin durumu, topun masaya göre tanımlı x ve y koordinatları ve her konumda hız bileşenleri v_x ve v_y ile belirlenir. Ayrıca, ıstaka topa öteleme hareketi ile beraber dönme hareketi de verir. Dönme ekseni iki ayrı koordinatla belirlenir. Dönme hızını da belirlemek için eksen gibi iki koordinata daha gereksinim vardır. Anlaşılacağı gibi, masa üzerinde basit bir hareket yapıyormuş gibi gördüğümüz bilardo topunun dinamiği, sekiz boyutlu bir uzayda tanımlanır. Masa üzerinde, yani iki boyutlu uzayda, hareket etmekte olan top esasında matematiksel olarak sekiz boyutlu bir uzayda hareket eder. İki veya üç boyutlu uzay geometrik olarak göz önünde canlandırılabilir. Üç ve üçten daha fazla boyuttaki uzaylar ancak matematiksel olarak kurgulanır. Bir sistemin dinamiğini veren bu cins uzaylara faz uzayı denir. Kaotik olayların deterministik hesapları genelde faz uzaylarında yapılır.

Kaotik sistemde denge eğrisi

Yukarıda iki balık türü hakkında verdiğimiz örneği lüfer ile hamsiler arasındaki yaşam zincirine uygulayalım. Esasında bu örnekte biyolojik bir kesinlik yoktur. Sadece iki canlı popülasyonu arasında bir denge durumunun oluşması açısından ilgi çeker. Karmaşaların yeterli bir süre sonra dengeye yaklaşmasını ve bir denge döngüsünün oluştuğunu gösterir. Belli bir koyda 2 bin tane lüfer buna karşı aynı koyda 200 bin hamsi bulunduğunu düşünelim. Şekil 3’te iki balık türü arasındaki yaşam döngüsü gösterilmiştir. Faz uzayındaki nokta başlangıç durumuna karşı gelir, yani 2 bin lüfer, 200 bin hamsi. Lüferler hamsi ile beslendiğinden (özel olarak bu koyda lüferler için başka bir besin kaynağı olmadığını kabul edelim) belli bir süre sonra hamsi sayısında bir azalma olurken lüfer sayısı ya sabit kalır ya da artar. Zaman ilerledikçe lüferler hamsi bulmakta zorlanacaklarından aralarında besin bulma savaşı başlar. Yeterince beslenemeyen, bu nedenle yeterince üreyemeyen lüfer sayısında bir azalma meydana gelir. Bir tarafta lüferlerden korkup kaçan, oraya buraya gizlenmiş hamsiler karşılarında çok sayıda lüfer olmadığından yeniden çoğalmaya başlarlar ve sonunda lüfer ve hamsi sayıları arasında faz uzayında çembere benzeyen, kapalı bir eğri ile temsil edilen bir denge durumu oluşur.

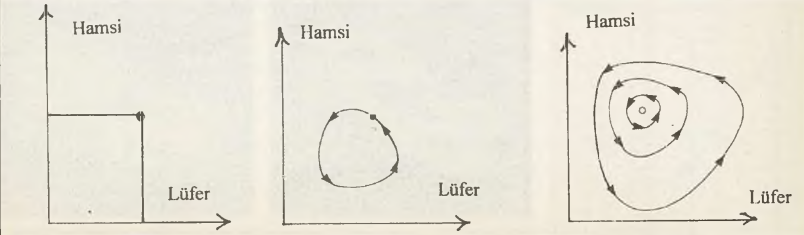
Şekil 3b’de bu durum gösterilmiştir. Şekil 3c’de ise farklı başlangıç şartları diğer denge eğrileri gösterilmiştir. Bu basit örnekten anlaşılacağı gibi iki balık türü arasındaki uzun süren ölüm kalım savaşı, sonunda faz uzayında bir denge eğrisi ile son bulur. Faz uzayının diğer bölgelerinde yer alan grafikler zamanla denge eğrisine yaklaşır. Sistemin dinamiği belli bir süre sonra denge eğrisini seçer. Karmaşık sistemlerin faz uzayına yansıyan denge eğrileri, deterministik kaos matematiğinin diğer bir yöntemini oluşturur. Sistem ne kadar kaotik olursa olsun, şayet tanımlanabilen başlangıç koşulları içeriyorsa, faz uzayında bir denge eğrisi ile temsil edilebilir.

Tam olarak periyodik olmayan fakat kendisini yaklaşık olarak tekrar eden hareketlerin benzeşim analizleri de deterministik kaos kuramlarının ilgi alanı içindedir. Örneğin, bir uydu yerküre etrafında dönerken yerküre güneş etrafında, güneş de galaksiye göre dönme hareketi yapar. Bu periyodik hareketlerin bileşimi olan hareket yukarıda belirttiğimiz gibi kendisini yaklaşık olarak tekrar eder. Benzer hareketlerin faz uzayına yansıtılan resmi birbirinden ayırt edilebilen dairesel denge eğrileri verir. Şekil 4'te çift daireli denge eğrisi gösterilmiştir. Resim hamsi-lüfer popülasyon ilişkisine benzer. Burada periyodik olamayan hareketlerin kaotik hareketleri analitik olarak incelenmemiştir. Önemli olan faz uzayında oluşan denge eğrilerinin anlaşılmasıdır.

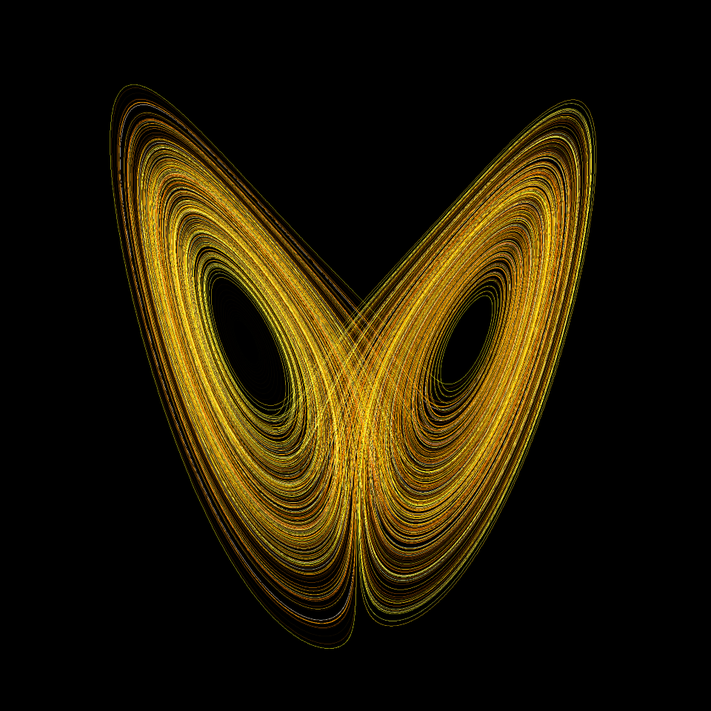
Şekil 4’te verilen lüfer ve hamsi arasındaki kaotik türünü sürdürme mücadeleleri her zaman geometrik olarak çizilebilen kapalı denge eğrileri ile sonuçlanmaz. Esasında av ve avcı arasında karmaşık bir düzen geçerlidir. Şekil 5’te böyle karmaşık bir sistemin zaman ilerledikçe değişimi, bilgisayar simülasyonu ile iki boyuta tanımlı popülasyon düzlemine indirgenerek gösterilmiştir. Yatay eksen av, düşey eksen avcı nüfusunu temsil etmektedir. Türlerin sayılarındaki oynaklık sarı renkli bölgede yoğunlaşmıştır. Değişim, bazı durumlarda kırmızı bölgelere kaymaktadır. Görüldüğü gibi matematik olarak elde edilen ve geometrik olarak çizilebilen kapalı denge eğrileri sadece ideal durumlara tekabül etmektedir. Kaotik hareketlerdeki determinizm klasik mekanikte olduğu gibi mutlak bir kesinlik göstermez. 

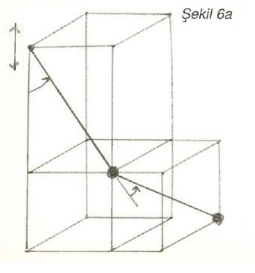
Yukarıda değişik bağlamlarda belirtildiği gibi dinamik sistemler genelde kaotik davranışlar içerir. Örneğin bağlantılı iki basit sarkacın hareketi, şayet birinci sarkacın bağlantı noktası bir dış etken nedeni ile aşağı yukarı bir titreşim yapıyorsa, kaotiktir. İkinci sarkaç birinci sarkaç ucuna Şekil 6’da gösterildiği gibi bağlanmıştır. Alttaki sarkaç, üst sarkaç salınımları ile 90 derecelik bir açı altında salınmaktadır. Üstteki sarkacın bağlantı noktasındaki aşağı yukarı titreşim frekansı değiştiğinde hareket ilginç bir karmaşa gösterir. Sistemi karakterize eden koordinatlar üst sarkacın düşeyle yaptığı açı, hızı ve dış etkenin salınım hızı ile alt sarkacın hızı ve düşeyle yaptığı açıdır. Görüldüğü gibi sistemi karakterize eden faz uzayı bu örnekte beş boyutludur. Faz uzayına yansıtılan resim, hareketi temsil eden diferansiyel denklemlerin art arda gelen çözümlerinin birbirlerini besleyerek bilgisayar ile çözümlerinden elde edilir. Önemli olan beş boyutta gerçekleşen kaotik hareketin resmini iki boyutlu uzaya yani düzleme indirgeyebilmektir. Şekil 6b'de faz uzayına yansıyan grafik verilmiştir.

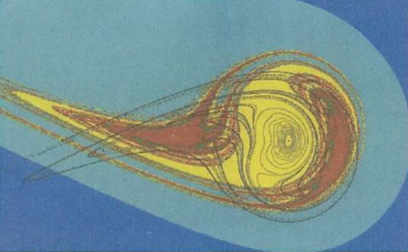
Faz uzayını belirleyen beş koordinat arasından konum belirleyen üç tanesini seçerek benzeşim programı ile hareket iki boyuta izdüşürülmüştür. Şekil 6b’deki soldaki resim, üst sarkacı aşağı yukarı salındıran sabit frekans altında sistemin denge eğrisini temsil eder. Farklı renkler alt ve üst sarkaçları gösterir. Resmin sol tarafı ise salınım frekansının değiştirilmesi durumunda denge eğrilerinin aldığı yapıyı gösterir. Esasında hareket çok karmaşıktır. Salınım frekansı değiştirildikçe sistem yerçekiminin etkisi altında çok daha karmaşık hareketler yapar. Bütün bu karmaşaya rağmen faz uzayı analizleri denge eğrilerini belirleyebilir. Şekil 7'de, çift sarkaç örneğinde olduğu gibi, periyodik zorlayıcı bir kuvvetin etkisi altında nonlineer (doğrusal olmayan) kaotik salınımlar yapan bir sistemin bilgisayar simülasyonu gösterilmiştir. Değişik renkler farklı salınım modlarına ait denge bölgelerini temsil eder.

Güneş sistemi ve mühendislikteki kaotik problemler

Güneş sisteminde gezegenlerin ölçülen ve Newton kanunlarına göre hesap edilen periyotlarının ölçüm hataları içinde örtüşmesi, bu sistemin tam olarak determinist olduğu şeklinde bir fikir uyandırır. Newton kanunlarına göre Ay'a gidebildik Mars'ın kimyasal yapısını analiz edebildik, daha uzak gezegenlere gitmeyi, uzayda koloniler kurmayı tasarlıyoruz. Ancak problem daha derinden analiz edildiğinde tıkır tıkır çalışan bu sistemin sanıldığı gibi determinist olmadığı, içinde bazı belirsizliklerin olduğu görülür. Newton kanunları karşılıklı olarak etkileşen iki kütle arasındaki çekim kuvvetinin kütleler arasındaki uzaklığın karesi ile ters, kütlelerin çarpımı ile doğru orantılı olduğunu söyler. Güneş sisteminde ise gezegenler kütle-çekim etkisi ile güneş etrafında dönerken aynı zamanda aynı kanununa göre birbirleri ile de etkileşirler. Sistem, güneş ve gezegen gibi iki parçacıktan oluştuğunda veya iki parçacıktan oluştuğu kabul edildiğinde, hareketi veren diferansiyel denklemlerin analitik çözümlerini bulmak mümkündür. Gezegenlerin hesaplanan periyotları bu denklemlerin çözümlerinden elde edilmiştir. Ancak bu kabul diğer gezegenlerin örneğin Jüpiter’in, yerkürenin hareketlerine bir etkisi olmadığını söyler. Bu ise kozmolojik gerçek ile çelişir. Hesaba diğer bir gezegeni örneğin Jüpiter'i eklerseniz ortaya iki değil üç parçacık problemi çıkar. Aynı anda kütle-çekim ile etkileşen üç parçacığın hareketlerini temsil eden diferansiyel denklemlerin analitik çözümleri yoktur. Yani bu noktada diferansiyel integral hesap tıkanır. Ünlü Fransız matematikçisi Laplace ömrünün önemli bir bölümünü gök mekaniğinin sonuçsuz kalan üç parçacık problemini çözmek için geçirmiştir. Esasında güneş sistemi sadece üç parçacıktan da ibaret değildir. Burada amacımız güneş sistemindeki kaotik olayların analizini yapmaktan çok kaosun nedenlerini aktarmaktır. Çok basit olarak incelediğimiz sarkaç salınımlarının kaotik hareketleri ile güneş sistemindeki kaotik hareketlerin analizleri arasında benzerlikler vardır.

Genel rölativite, evrenin kütle-çekim etkisi ile nasıl analiz edilmesi gerektiğini söyler. Söz konusu kütleler galaksiler, yıldızlar gibi devasa oluşumlardır. Ancak evren sadece makroskopik kütlelerden ibaret değildir. Madde atomik boyutlarda yapılaşan sistemlerin bir toplamıdır. Maddeyi oluşturan bölünemeyen en küçük yapı taşlarının neler olduğunu standart model verir. Büyüklükleri bir metrenin on milyarda biri kadar küçük olan bu yapılanmaların dinamiğini ise kuantum mekaniği belirler. Yukarıda belirtildiği gibi Newton mekaniği her ne kadar birinci yaklaşım ile deterministik bir kuram ise de kaotik olaylardan soyutlanmış değildir. Kuantum mekaniği ise probabilistik bir kuramdır ve kuramın kaotik komponentleri probabilité kavramı üzerinde kurgulanır.

Atomik boyutlarda çevresinden soyutlanmış bir sistemin enerjisi klasik fizikte olduğu gibi sürekli değerler almaz. Sistemi belirleyen tüm fiziksel büyüklükler, enerjide olduğu gibi, belli seçim kurallarına uygun, kesikli değerler alır. Dolayısıyla kuantum mekanik bir sistem, sistemi belirleyen fiziksel büyüklüklerin kesikli değerleri ile tanımlıdır. En düşük enerji seviyesine temel seviye denir ve bir dış pertürbasyon (sapma) olmadığı sürece sistem bu seviyede bulunur. Temel seviyenin üstündeki seviyelere uyarılmış seviyeler denir. Kuantum mekaniğinin keyfiliği veya karmaşıklığı klasik fiziğin karmaşıklığından farklıdır. Klasik fizikte karmaşıklık Newton yörüngelerindeki keyfilikten kaynaklanır. Kuantum mekaniğinde ise sistemin dinamiğini tanımlayan bir yörünge mevcut değildir. Bir laser demetini oluşturan fotonlardan hangisi ne zaman, nerede bulunur bilinemez. Belirsizlik ilkesi kuantal boyutlarda bir parçacığın hızı ve konumunun aynı anda belirlenemeyeceğini dikte eder. Bütün fiziksel büyüklerin teorik değerleri ancak belli bir olasılıkla verilir. Olasılık ise Schrödinger denklemlerinin çözümü olan dalga fonksiyonları ile tanımlıdır. Kuantum mekanik olasılıklar makroskopik boyutlarda klasik fiziğin tanımladığı değerlere limit olarak yaklaşır. Kuantum mekaniği ve klasik fizik arasındaki bu tekabüliyet ilkesi akla kuantal sistemlerin limit durumlarda Newtonian kaosunu içerip içermediği sorusunu getirir. Kuantum mekanik kaos ile klasik fizik kaos arasındaki farklar ünlü nonlineer optik uzmanı Prof. Dr. Giulio Casati ve grubu tarafından belirlenmiştir. (Profesör Casati ile European Science Foundation yönetim kurulunda 6 sene beraber çalıştım. Kendisi keskin zekası ve olaylara özgün bakış açısı ile çevresini etkileyen bir teorik fizikçidir. Kanımca nonlineer olayların tartışmasız önde gelen uzmanlarından biridir.) Kuantum mekaniğinde beliren kaotik olayların ayrıntılı analizleri bu makalenin kapsamı dışındadır.

Akademik ilginin dışında, sistemlerin kaotik davranışları mühendisliğin kararlı sistemler tasarlamasının önünde en önemli engeli oluşturur. Enerji nakil hatlarından alınan akımın akım-voltaj eğrilerinde gözlenen karmaşık değişimleri veya nonlineer amplifikatörlerde geri beslemeye rağmen akım profilinin kendini tekrar eden bir grafik çizmemesi veya bir gemiyi kararsız denge durumuna getiren şartların belirsizliği, meteoroloji ve bulut dinamiği, mühendislikte karşılaşılan kaotik problemlerden bazılarıdır ve her birisi ayrı bir makale konusu olacak kadar kapsamlıdır. Burada sadece kaotik olaylarda gözlenen bazı düzenli davranışlar üzerinde durulmuştur.

Türbülans, akışkanlarda oluşan ve dinamiği bilinemeyen bir doğa olayıdır. Uçak yolculuklarında sık sık rastlanır. Havanın veya genel anlamda bir akışkanın merkezcil bir nokta etrafında kararsız bir dönme hareketi yapmasıdır. Matematiksel bir model ile belirlenmesi mümkün görülmemektedir, iklimde son 100 yıl içinde yaşanan değişimler, özellikle küresel ısınma, okyanuslar üzerinde meydana gelen kasırgaların sayısında artışlara neden olmuştur. 100 seneyi aşkın bir süredir akışkan mekanikçileri ve uygulamalı matematikçiler türbülans dinamiğinin nedenlerini anlamaya çalışmaktadırlar. Ancak bütün bu gayretlere rağmen türbülanslar gizemlerini korumaktadır. Akışkanların sıkıştırılamaz olduğu, sıcaklığının sabit olduğu, akışkan hız ve basıncının zamana bağlı olamadığı, akışkanın çalkantılı değil laminar olduğu, viskositenin (akmazlık) dinamiğe etki etmediği kabulleri altında elde edilen Bernoulli ve Stokes kanunları ile türbülans açıklanamamıştır. Ancak akışkanın kütlesi, hızı ve viskositesi ile tanımlanan parametreler cinsinden akışkan dinamiğinde bazı deterministik özellikler tespit edilebilmiştir.

Bu yazı Bilim ve Ütopya'nın Kasım 2006 sayısında yayımlanmıştır.